聚合物发泡过程和发泡机理
聚合物发泡成型过程一般包括三个基本阶段:聚合物/气体均相体系的形成、气泡的成核、泡孔的生长和定型。第一阶段是在一定的温度和压力下,气体通过扩散进入聚合物基体内,经过一段时间后达到溶解平衡状态形成聚合物/气体均相饱和体系。第二阶段是泡孔成核,体系的热力学不稳定性是泡孔成核的主要驱动力。诱导均相饱和体系中出现热力学不稳定性可以通过调控发泡压力(骤降)和温度(升),进而改变气体在溶液中的溶解度来实现。当体系出现热力学不稳定性后,体系处于过饱和状态,聚合物与气体将会发生相分离,促进泡孔成核。第三阶段是泡孔的生长和成型。在泡孔成核后,聚合物基体中溶解的气体会扩散至泡孔核中并使泡孔核直径增加。泡孔生长的过程是气体不断消耗和减少的过程。在一定时间后,体系中没有足够的气体来维持泡孔继续生长,即泡孔生长驱动力降低。随着生长时间的增加,温度不断下降,聚合物熔体粘弹性增强,聚合物分子链的运动能力降低,泡孔生长阻力增加,最终泡孔生长停止,泡孔结构和密度趋于稳定。泡孔生长速率受界面张力、气体扩散速率、聚合物粘弹性、结晶性能等因素的影响。通过对发泡机理进行深入探究,可以改善和优化聚合物的生产过程,进而提高聚合物发泡性能。

Figure 2. Schematic diagram of supercritical fluid foaming.
聚合物/气体均相体系的形成
聚合物/气体均相体系的形成是在一定的温度和压力下,通过适当的方法将惰性气体(如CO2或者N2)扩散溶解在聚合物中,形成均匀的聚合物/气体饱和体系。在饱和阶段,聚合物表面的压力梯度引起两种现象:聚合物内气体的溶解和扩散。后者速度较慢,因此更具动力学决定性。

Figure 3. Solubilities of CO2 in PLA at various temperatures and pressures. x1 is the mass fraction (wt%) of CO2 in PLA melt. The scatter dots at different temperatures (463 k, 333 k, 308 k) are the experimental data.
压力的增加可能会提高二氧化碳的最大溶解度。Yu等人利用动态密度泛函理论研究了CO2在PLA熔体中的溶解行为,发现溶解度随着压力的增加而增加。
泡孔的成核
成核是指在热力学不稳定驱动下,溶解在初始相中的第二相分子聚集形成稳定的第二相的过程。当超临界流体溶入聚合物中形成均相体系后,由于体系温度升高或压力下降导致体系处于过饱和态,在聚合物基体中大量气泡形成使得体系到达低能量的稳定态。

Figure 4. (a) Bubble nucleation and growth as a function of free energy, (b) contact angle and semi-conical angle for heterogeneous bubble nucleation.
均相成核涉及在胚胎形成阶段无异物或添加剂(异质成核剂-NA)或预先存在的泡孔核的情况下自发和随机形成泡孔。它通常是对温度或压力的随机波动或变化的反应而响应的。理论上,每个分子都可以作为成核位点,从而在均匀成核中产生最理想的成核密度和泡孔尺寸半径。但由于缺乏成核剂的诱导,成核所需的自由能较高,这就要求体系具有较大的过饱和度。
当在连续聚合物气相和第三相之间的界面处形成核时,就会出现异相成核,这是由作为成核中心的成核剂引发的,而不是自发的(见图4b)。成核剂包括填料和晶体,它们通过提供异质表面来降低成核能垒,从而提高成核密度。

Figure 5. Cellular morphology of PLLA foams prepared under different foaming temperatures: (a1, a2) 90 °C; (b1, b2) 100 °C; (c1, c2) 105 °C; (d1, d2) 110 °C; (e1, e2) 115 °C; (f1, f2) 120 °C.

Figure 6. Cellular morphology of D2.5 foams prepared under different foaming temperatures: (a1, a2) 90 °C; (b1, b2) 100 °C; (c1, c2) 105 °C; (d1, d2) 110 °C; (e1, e2) 115 °C; (f1, f2) 120 °C.
Yu等人使用超临界CO2研究了纯聚(L-乳酸)(PLLA)和PLLA/聚(D-乳酸)(PDLA)的发泡特性。结果表明,立体络合物晶体可以作为成核位点,有效降低成核能垒,导致PLLA/PDLA泡沫样品的泡孔密度显著增加,泡孔直径减小。
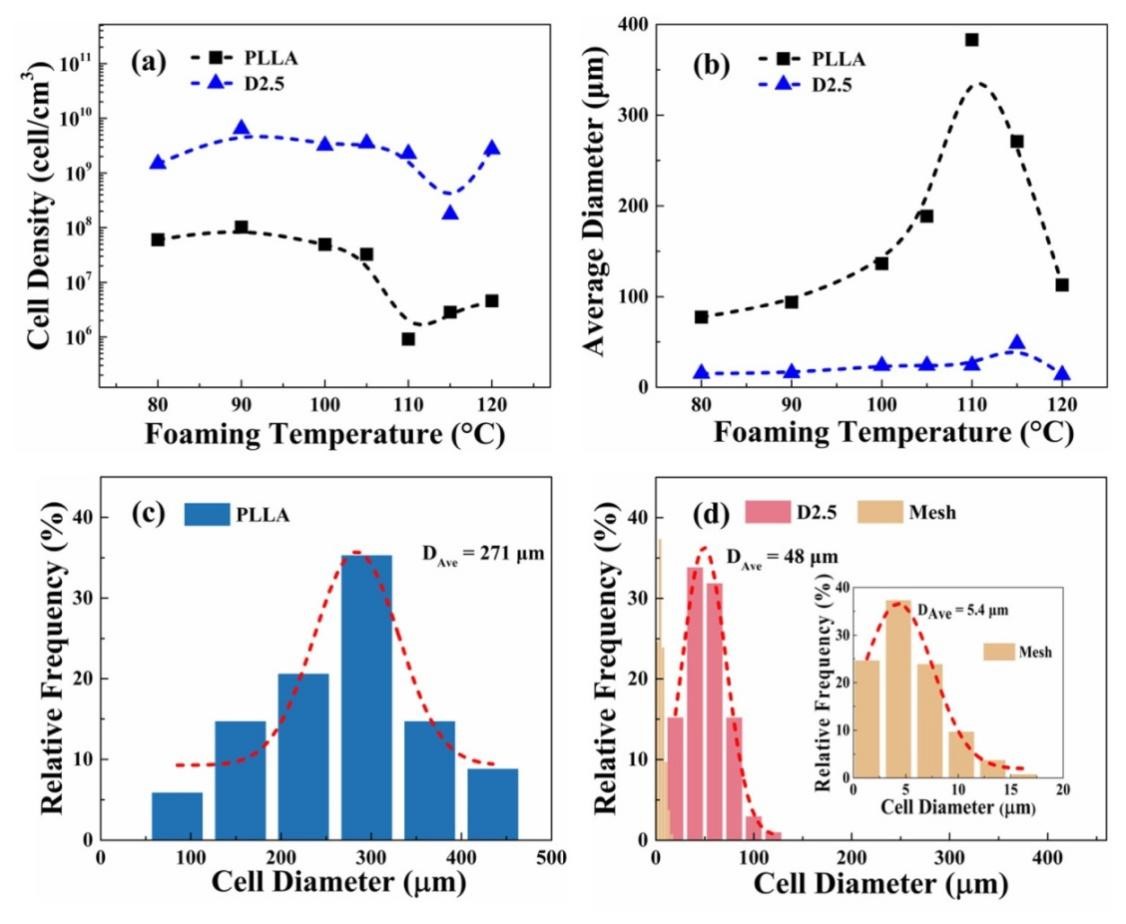
Figure 7. (a) Cell density; (b) average diameter of PLLA and D2.5 foams under different foaming temperatures; (c) cell size distribution of PLLA foams prepared at 115 °C; (d) cell size distribution of D2.5 foams prepared at 115 °C (the insert figure shows the cell size distribution of mesh-like holes)
泡孔的生长
(1) 利用经验公式计算气泡半径
在 1950 年,Epstein 和 Plesset通过对静态聚合物熔体中气泡长大过程的研究,得到了气泡长大随时间的变化关系式:
 (14)
(14)
其中,R:气泡半径;D:气体的扩散系数;α:与气体浓度和压力等有关的系数。
(2) 海岛模型
海岛模型是指单个气泡在一个充满无限量聚合物熔体的矩形模腔内长大的物理模型。该模型通过了解单个气泡的长大过程来描述整个体系中气泡的生长规律。

Figure 8. Island model
Papanstasiou 和 Scriven (J. Non-Newtonian Fluid Mech., 1984)在海岛模型的基础上,利用数值计算方法来研究分析单个球形气泡在无限量聚合物熔体中的长大和破裂过程。
(3) 细胞模型
由于用单个气泡在无限大熔体中的增长过程来表征整个体系气泡的膨胀规律与实际情况有偏差,用海岛模型进行推算必然会带来误差。Amon等(Polymer Engineering & Science,1984)提出了细胞模型,该模型是含有无数气泡的聚合物熔体划分为同样数量的泡壳单元,每个单元含有同样的熔体质量,都包含一个球型的气泡内核及同心的熔体外壳,熔体外壳中处于过饱和状态的气体不断扩散入气泡内,从而气泡不断长大。由于泡壳模型反映出发泡膨胀体系的真实条件,较好地解决了相互邻近的气泡在膨胀过程中的相互作用,普遍被研究者们接受。
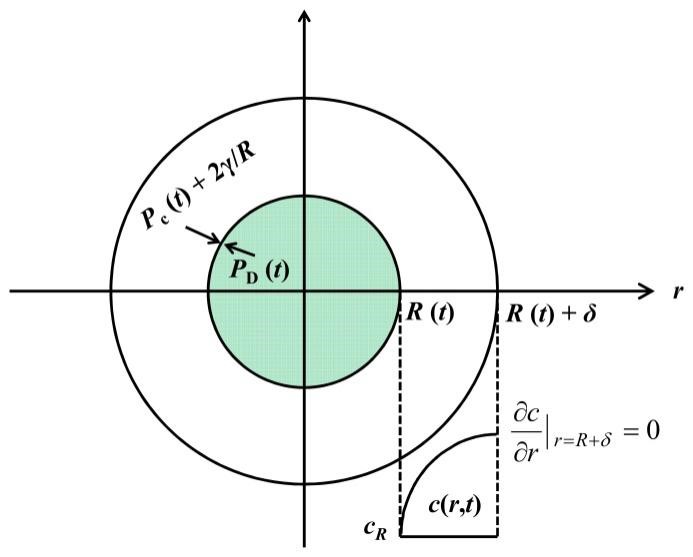
Figure 9. Schematic of cell model.